4.4 집합 커버 문제
1. 문제
n개의 원소를 가진 집합인 U가 있고, U의 부분 집합들을 원소로 하는 집합 F가 주어질 때, F의 원소들인 집합들 중에서 어떤 집합들을 선택하여 합집합하면 U와 같게 되는가?
집합 커버(Set Cover) 문제는 F에서 선택하는 집합들의 수를 최소화하는 문제이다.
- 예시 - 신도시를 계획함에 있어서 학교를 배치하는 문제

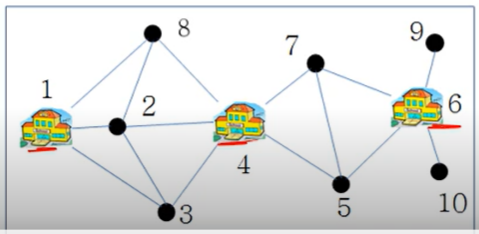
위 그림과 같이 신도시에 10개의 마을이 만들어질 계획이다.
이 때, 아래의 2가지 조건이 만족되도록 학교의 위치를 선정하여야 한다고 가정한다
- 학교는 마을에 위치한다.
- 등교 거리는 걸어서 15분 이내여야 한다.
어느 마을에 학교를 신설해야 학교의 수가 최소로 될 것인가?
2번 마을에 학교를 만들면 마을 1, 2, 3, 4, 8이 커버된다.
또한, 6번 마을에 학교를 만들면 마을 5, 6, 7, 9, 10이 커버된다.
즉, 2번과 6번을 선택하면 학교 수를 최소로 신설할 수 있다.

위 신도시 계획 문제를 집합 커버 문제로 변환하면 아래와 같다.
U = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} // 신도시의 마을 10개
F = {S1, S2, S3, S4, S5, S6, S7, S8, S9, S10}
S1 = {1, 2, 3, 8}
S2 = {1, 2, 3, 4, 8}
S3 = {1, 2, 3, 4}
S4 = {2, 3, 4, 8}
S5 = {4, 5, 6, 7}
S6 = {5, 6, 7, 9, 10}
S7 = {4, 5, 6, 7}
S8 = {1, 2, 4, 8}
S9 = {6, 9}
S10 = {6, 10}
Si 집합들 중에서 어떤 집합들을 선택하여야 그들의 합집합이 U와 같은가?
(단, 선택된 집합의 수는 최소이어야 한다.)
답은 S2 ∪ S6 = {1, 2, 3, 4, 8} ∪ {5, 6, 7, 9, 10} = {1, 2, 3, 4, 5, 6, 7, 8, 9 10} = U
집합 커버 문제의 최적해를 찾는 가장 간단한 방법은 F에 있는 집합들의 모든 조합을 하나씩 합집합하여 U가 되는지 확인, U가 되는 조합의 집합 수가 최소인 것을 찾는 것이다.
그런데 이 경우 F에 n개의 원소가 있으면 (2n-1)개를 다 검사, n이 커지면 최적해를 찾는 것은 실질적으로 불가능하다.
이를 극복하기 위한 방법은 최적해를 찾는 대신 최적해에 근사한 근사해(Approximation Solution)를 찾는 것이다.
-> 가장 많은 원소를 포함하고 있는 아이부터 선택 (그리디하게)
2. 알고리즘
다음은 집합 커버 문제를 위한 근사 알고리즘이다.
SetCover
입력: U, F={Si}, i=1,2,...,n
출력: 집합 커버 C
C = ∅
while (U ≠ ∅) do {
U의 원소들을 가장 많이 포함하고 있는 집합 Si를 F에서 선택한다.
U = U - Si
Si를 F에서 제거하고, Si를 C에 추가한다.
}
return C
위 신도시 계획 문제에 이 알고리즘을 적용한다.
- Line 4 : C = ∅로 초기화한다.
- Line 5 : while-조건 (U ≠ ∅)을 만족한다.
- Line 6 : U의 원소들을 가장 많이 커버하는 집합인 S4를 F에서 선택한다.
- Line 7 : U - S4 = {1, 6, 9, 10}
- Line 8 : S4를 F에서 제거, 즉, F = {S1, S2, S3, S5, S6, S7, S8, S9, S10},
S4를 C에 추가, 즉, C = {S4} - Line 5 : while-조건 만족
- Line 6 : U의 원소들을 가장 많이 커버하는 집합인 S6를 F에서 선택.
- Line 7 : U = S6 = {1] -> 공집합이 아님
- Line 8 : S6를 F에서 제거, F = {S1, S2, S3, S5, S7, S8, S9, S10},
S6를 C에 추가, C = {S4, S6} - Line 5 : while-조건 만족
- Line 6 : U의 원소들을 가장 많이 커버하는 집합인 S1을 F에서 선택.
(S2, S3, S8을 선택해도 무방) - Line 7 : U = ∅
- Line 8 : S1을 F에서 제거,
S1을 C에 추가, C = {S1, S4, S6} - Line 5 : while-조건 불만족
- Line 9 : C={S1, S4, S6}를 리턴
3. 시간 복잡도
Line 5 : while-루프 조건 검사 시간 O(1)
Line 6 : Si 각각을 U와 비교하여야 한다. Si들의 수가 최대 n이라면, O(n^2) 시간
Line 7 : 집합 U에서 집합 Si의 원소를 제거, O(n) 시간이 걸린다.
Line 8 : Si를 F에서 제거, Si를 C에 추가, O(1) 시간이 걸린다.
따라서 루프 1회의 시간 복잡도는 O(1)+O(n^2)+O(n)+O(1) = O(n^2)이다.
그러므로 SetCover 알고리즘의 시간복잡도는 O(n)*O(n^2) = O(n^3)
4.5 작업 스케줄링
1. 문제
기계에서 수행되는 n개의 작업 t1, t2, … tn이 있고, 각 작업은 시작시간과 종료시간이 있다.
작업 스케줄링(Task Scheduling) 문제는 작업의 수행 시간이 중복되지 않도록 모든 작업을 가장 적은 수의 기계에 배정하는 문제이다.
1-1) 예시 - 학술대회에서 발표자들을 강의실에 배정하는 문제
작업 스케줄링 문제에 주어진 문제 요소들은 작업의 수, 각 작업의 시작시간과 종료시간이다.
작업의 시작시간과 종료시간은 정해져 있으므로 작업의 길이도 주어진 것이다.
그리하여 시작시간, 종료시간, 작업 길이에 대해 다음과 같은 그리디 알고리즘들을 생각할 수 있다.
- 빠른 시작시간 작업을 우선(Earliest start time first) 배정 -> 최적해O
- 빠른 종료시간 작업을 우선(Earliest finish time first) 배정 -> 최적해X
- 짧은 작업 우선(Shortest job first) 배정 -> 최적해
- 긴 작업을 우선(Longest job first) 배정 -> 최적해
위 4가지 알고리즘들 중 첫 번째 알고리즘을 제외, 나머지 3가지 알고리즘은 항상 최적해를 찾지 못한다.
2. 알고리즘
다음은 작업 스케줄링 문제를 위한 빠른 시작시간 작업을(Earilest start time first) 우선 배정하는 그리디 알고리즘이다.
JobScheduling
입력: n개의 작업 t1, t2, ... , tn
출력: 각 기계에 배정된 작업 순서
시작시간의 오름차순으로 정렬한 작업 리스트를 L이라고 한다.
while (L ≠ ∅) {
L에서 가장 이른 시작시간을 가진 작업 ti를 가져온다.
if (ti를 수행할 기계가 있으면)
ti를 수행할 수 있는 기계에 배정한다.
else
새로운 기계에 ti를 배정한다.
ti를 L에서 제거한다.
}
return 각 기계에 배정된 작업 순서
t1 = [7,8],
t2 = [3,7],
t3 = [1,5],
t4 = [5,9],
t5 = [0,2],
t6 = [6,8],
t7 = [1,6]
과 같은 작업 이 있다고 가정한다. 단, [s,f]에서 s는 시작시간, f는 종료시간이다.
- Line 4 : L = {[0,2], [1,6], [1,5], [3,7], [5,9], [6,8], [7,8]}이다.
- Line 5~11 : while-루프를 반복 수행하면서 각 작업이 적절한 기계에 배정된다.
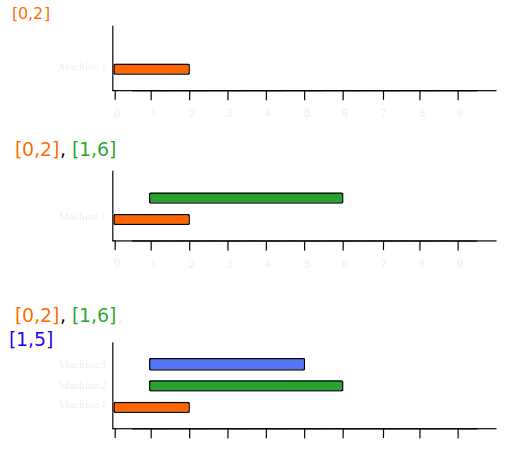
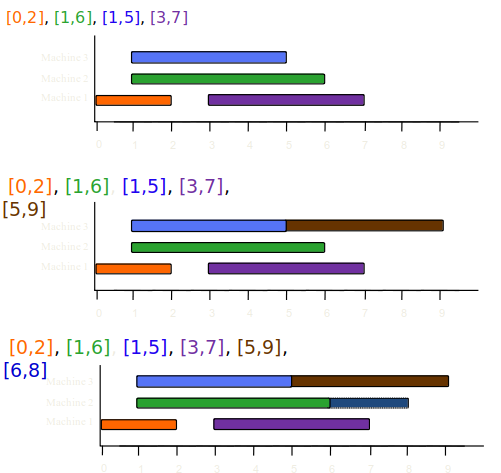
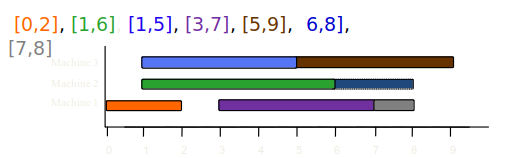
이 경우 최적해는 3대의 기계에 모든 작업을 마지막 그림과 같이 배정하는 것이다.
3. 시간복잡도
Line 4에서 n개의 작업을 정렬하는 데 O(nlogn) 시간이 걸린다.
while-루프에서 작업을 L에서 가져다가 수행 가능한 기계를 찾아 배정하므로 O(m)이 걸린다.
(m은 사용된 기계의 수)
while-루프가 수행된 총 횟수는 n번이므로, line 5~12까지는 O(m)*n = O(mn) 시간이 걸린다.
따라서 O(nlogn) + O(nm)이다.
4.6 허프만 압축
1. 허프만 압축
파일의 각 문자가 8bit 아스키(ASCII) 코드로 저장되면, 그 파일의 bit 수는 8 * (파일의 문자수)이다.
즉, 파일의 각 문자는 고정된 크기의 코드로 표현된다.
이러한 고정된 크기의 코드로 구성된 파일을 저장하거나 전송할 때 파일의 크기를 줄이고, 필요시 원래의 파일로 변환할 수 있으면,
메모리 공간을 효율적으로 사용할 수 있고, 파일 전송 시간을 단축시킬 수 있다.
주어진 파일의 크기를 줄이는 방법을 파일 압축(file compression)이라고 한다.
허프만(Huffman) 압축은 파일에 빈번히 나타나는 문자에는 짧은 이진 코드를 할당, 드물게 나타나는 문자에는 긴 이진 코드를 할당한다.
허프만 압축 방법으로 변환시킨 문자 코드들 사이에는 접두부 특성(Prefix Property)이 존재한다.
이는 각 문자에 할당된 이진 코드는 어떤 다른 문자에 할당된 이진 코드의 접두부가 되지 않는다는 것을 의미.
즉, 문자 ‘a’에 할당된 코드가 ‘101’이라면, 다른 모든 문자의 코드는 ‘101’로 시작되지 않으며 또한 ‘1’이나 ‘10’으로도 시작되지 않는다.
접두부 특성을 가진 코드의 장점은 코드와 코드 사이를 구분할 특별한 코드가 필요 없다는 것이다.
예를 들어. 101#100#0#111#…에서 ‘#’이 인접한 코드를 구분 짓는데, 허프만 압축에서는 이러한 특별한 코드가 필요 없이 파일을 압축 및 해제할 수 있다.
허프만 압축은 입력 파일에 대해 각 문자의 출현 빈도수에 기반을 둔 이진트리를 만든 뒤, 각 문자에 이진 코드를 할당한다. 이 때, 이 이진 코드를 허프만 코드라고 한다.
2. 알고리즘
다음은 파일 압축을 위한 허프만 코드를 찾기 위한 그리디 알고리즘이다.
입력 파일에 대해 각 문자에 할당될 이진 코드를 추출할 이진 트리인 허프만 트리를 리턴한다.
HuffmanCoding
입력: 입력 파일의 n개의 문자에 대한 각각의 빈도수
출력: 허프만 트리
각 문자에 대해 노드를 만들고, 그 문자의 빈도수를 노드에 저장한다.
n개의 노드들의 빈도수에 대해 우선순위 큐 Q를 만든다.
while (Q에 있는 노드 수 >=2) {
빈도수가 가장 작은 2개의 노드(A와 B)를 Q에서 제거한다.
새 노드 N을 만들고, A와 B를 N의 자식 노드로 만든다.
노드 N을 Q에 삽입한다.
}
return Q // 허프만 트리의 루트를 리턴하는 것이다.
예시)
입력 파일이 4개의 문자로 구성되어 있고, 각 문자의 빈도수는 다음과 같다고 가정한다.
A: 450 T: 90 G:120 C:270
- Line 5 : 4개의 문자들의 빈도수에 대해 우선순위 Q를 만든다.

- Line 6 : while-루프 조건이 ‘참’이므로, Line 7~10을 수행한다.
즉, Q에서 ‘T’와 ‘G’를 제거한 후, 새 부모 노드를 Q에 삽입한다.
- Line 6 : while-루프 조건 ‘참’, Line 7~10을 수행.
즉, Q에서 ‘T’와 ‘G’의 ‘부모 노드’와 ‘C’를 제거한 후, 새 부모 노드를 Q에 삽입한다.
- Line 6 : while-루프 조건 ‘참’, Line 7~10을 수행.
즉, Q에서 ‘c’의 ‘부모 노드’와 ‘A’를 제거한 후, 새 부모 노드를 Q에 삽입한다.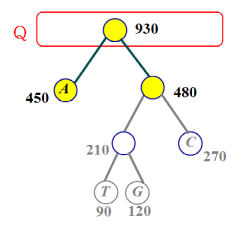
- Line 6 : while-루프 조건 ‘거짓’, Line 11에서 Q에 있는 노드를 리턴.
즉, 허프만 트리의 루트가 리턴된다.
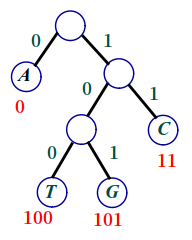
반환한 트리를 보면, 문자는 leaf 노드에만 존재한다.
루트로부터 왼쪽 자식 노드로 내려가면 ‘0’, 오른쪽 자식 노드로 내려가면 ‘1’을 부여할 수 있다.
그리하여 leaf 노드에 도착할 때까지 이진수를 추출, 문자의 이진코드를 구할 수 있다.
빈도수가 가장 높은 ‘A’는 가장 짧은 코드인 ‘0’,
빈도수가 가장 낮은 ‘T’는 가장 긴 코드인 ‘100’이 부여됐다.
또한 이렇게 얻은 숫자에 대한 코드는 접두부 특성을 가지고 있다.
(왜냐하면, leaf 노드에만 문자가 있고, 내부 노드에는 문자 없으며 코드를 부여하지 않았기 때문)
위 예제에서 압축된 파일의 bit 수는 (450*1)+(90*3)+(120*3)+(270*3) = 1620 bit이다.
반면에 아스키 코드로 된 파일 크기는 (450+90+120+270)*8 = 7440 bit이다.
압축률은 (1620/7440)*100 = 21.8%이다.
line 4, n개의 노드생성, 각 빈도수를 노드에 저장, O(n)
line 5, n개의 노드로 우선순위 큐 Q를 만듬. 힙 자료 구조 사용, O(n)
line 6~10, 노드 2개를 Q에서 제거, 새 노드를 Q에 삽입하므로 O(long), while-루프는 (n-1)번 반복, (n-1)*O(logn) = O(nlogn)
line 8, 트리의 루트를 리턴, O(1)
따라서 HuffmanCoding의 알고리즘은 O(nlogn)
Reference
NoName, IT blog
2020-02-02 1. 웹 애플리케이션2. JSP, Servlet, Spring 1. 웹 애플리케이션 웹 시스템 정적 컨텐츠 : 클라이언트 머신의 웹 브라우저가 네트워크에 있는 웹 서버로부터 요청한 HTML을 읽어와 표시 동적 컨텐
dudri63.github.io
'알고리즘 > 알고리즘' 카테고리의 다른 글
| [알고리즘] 9. 해 탐색 알고리즘 (0) | 2022.05.29 |
|---|---|
| [알고리즘] 7. NP-완전 문제 (0) | 2022.05.10 |
| [알고리즘] 4. 그리디 알고리즘 (1) (0) | 2022.04.05 |
| [알고리즘] 3. 최근접 점의 쌍 찾기 알고리즘 (3) (0) | 2022.03.29 |
| [알고리즘] 3. 선택 문제 알고리즘 (2) (0) | 2022.03.29 |
![[알고리즘]4. 그리디 알고리즘(2)](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FbywMLB%2Fbtrzacmwvgj%2FV2mgwMEvzr37wiHr3noHW1%2Fimg.png)